2 min to read
What is Algorithm?
이 글은 Edwith에서 제공하는 모두를 위한 컴퓨터 과학 (CS50 2019)를 수강하고 정리한 글입니다.
Computer Science
컴퓨터 과학은 문제해결에 대한 학문입니다. 문제 해결은 입력(Input) 을 전달받아 출력(Output) 을 만들어내는 과정입니다.
이러한 입력과 출력을 표현하기 위해선 우선 모두가 동의할 약속(표준)이 필요합니다. 따라서 컴퓨터 과학 분야에서 가장 첫 번째 개념은 데이터를 어떻게 표현하는지에 대한 표현 방법입니다.
Representation of Information
우리는 컴퓨터를 통해 다양한 정보를 처리하게 됩니다. 간단한 숫자부터 시작해서 문자, 사진, 영상, 음악까지 정보를 표현하는 형태는 매우 다양합니다. 하지만 컴퓨터는 2진법과 같이 오직 0과 1로만 정보를 표현할 수 있습니다.
따라서 문자, 사진과 같은 숫자로 표현할 수 없는 정보를 2진법의 형태, 즉 0과 1로 정보를 표현하기 위해서는 ASCII, UNICODE, RGB같은 약속체계를 통하여 숫자로 표현하였습니다.
What is Algorithm?
우리는 이제 컴퓨터가 숫자, 문자, 색깔 등의 정보를 0과 1로 표현할 수 있다는 것을 알게되었습니다. 이를 통하여 알고리즘은 입력(input)에서 받은 정보를 출력(output)형태로 만드는 처리 과정을 뜻합니다.
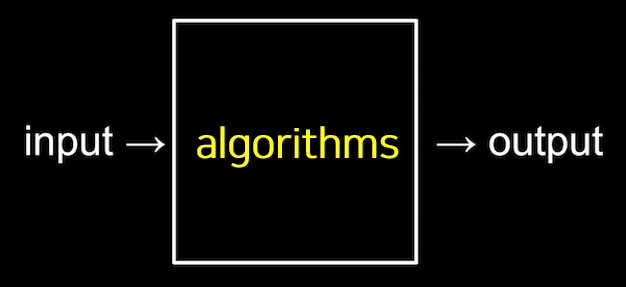
즉, 알고리즘이란 입력값을 출력값의 형태로 바꾸기 위해 어떤 명령들이 수행되어야 하는지에 대한 규칙들의 순서적 나열입니다.
이러한 일련의 순서적 규칙들을 어떻게 나열하는지에 따라 알고리즘의 종류가 달라집니다. 같은 출력값이라도 알고리즘에 따라 출력을 하기까지의 시간이 다를 수 있습니다.
Big-O Notation
알고리즘이 순서적 규칙 나열방법에 따라 종류가 달라지게 되면서 정확도와 효율성을 고려하게 되었습니다. 정확도란 주어진 입력에 대해서 올바른 출력을 뜻하고, 효율성이란 문제를 해결하기 위해 계산에 필요한 자원을 시공간적 측면에서 최소화 하는 것을 뜻합니다.
효율성은 시간 복잡도, 공간 복잡도로 이루어지게 되는데 통틀어서 알고리즘 복잡도로 불리기도 합니다. 시간 복잡도는 알고리즘이 문제를 해결하기 위해 수행한 시간(연산의 횟수)에 대한 개념이고, 공간 복잡도는 알고리즘이 얼마나 메모리 공간을 효율적으로 사용하는지에 대한 개념입니다
Big-$O$ 표기법은 알고리즘의 효율성을 시간 복잡도 관점에서 평가하기 위해 나타나게 되었습니다. 여기서 $O$는 “on the order of”의 약자로, 쉽게 생각하면 “~만큼의 정도로 커지는” 것이라고 볼 수 있습니다
아래의 그림과 같이 알고리즘을 실행하는데 걸리는 시간을 표현할 수 있습니다.
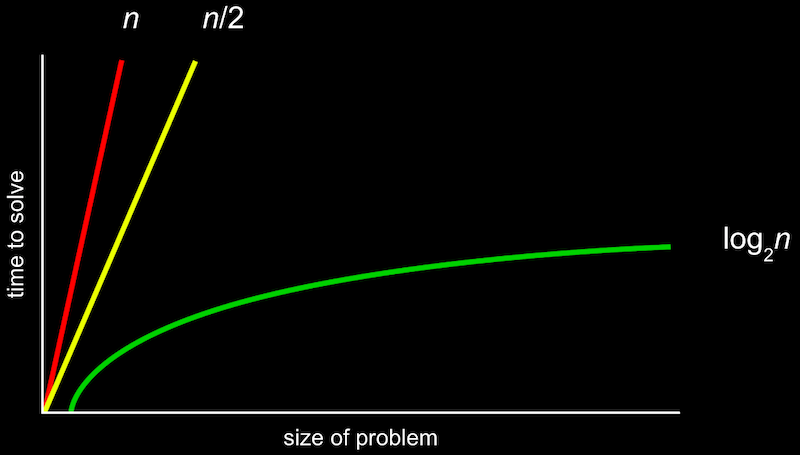
시간복잡도에서 중요하게 보는것은 가장 큰 영향을 미치는 $n$의 단위입니다. O($n$) 은 $n$만큼 커지는 것이므로 $n$이 늘어날수록 선형적으로 증가하게 됩니다. O($n/2$)도 결국 $n$이 매우 커지면 1/2은 큰 의미가 없어지므로 O($n$)이라고 볼 수 있습니다.
아래표는 실행시간이 빠른순으로 입력 $N$값에 따른 서로 다른 알고리즘의 시간복잡도입니다.
| Complexity | 1 | 10 | 100 |
|---|---|---|---|
| $O(1)$ | 1 | 1 | 1 |
| $O(log N$) | 0 | 2 | 5 |
| $O(N$) | 1 | 10 | 100 |
| $O(N log N$) | 0 | 20 | 461 |
| $O(N^2$) | 1 | 100 | 10000 |
Big $O$가 알고리즘 실행 시간의 상한을 나타낸 것이라면, 반대로 Big $\Omega(1)$는 알고리즘 실행 시간의 하한을 나타내는 것입니다.
예를 들어 선형 검색에서는 $n$개의 항목이 있을때 최대 $n$번의 검색을 해야 하므로 상한이 $O(n)$이 되지만 운이 좋다면 한 번만에 검색을 끝낼수도 있으므로 하한은 $\Omega(1)$이 됩니다.
Next
[Algorithm] Linear Search & Binary Search
[Algorithm] Bubble Sort & Selection Sort
- [Algorithm] Merge Sort
Comments