5 min to read
음성인식 입문하기
사람은 소리를 어떻게 인식하는가?
위키피디아에 따르면 소리 또는 음(音) 또는 ‘음파’는 공기나 물 같은 매질의 진동을 통해 전달되는 종파라고 합니다. 대표적으로 사람의 청각기관을 자극하여 뇌에서 해석되는 매질의 움직임이 그 예이다.
우리들의 귀에 끊임없이 들려오는 소리는 공기 속을 전해오는 파동입니다. 소리는 우리들에게 여러 가지 정보를 전해준다. 눈에는 보이지 않는 파동이지만 파동의 여러 가지 성질은 음파의 경우 귀에 들리는 소리의 변화로 알 수가 있다.
사람이 소리를 들을 수 있는 것도 공기가 진동하기 때문입니다. 즉 주파수(진동수)를 가지기 때문입니다.
우리가 듣는 소리는 실제로 진동이며, 이 진동이 청각기관을 통하여 뇌에서 소리로 알아듣기 위해서 아래와 같은 과정을 거치게 됩니다.
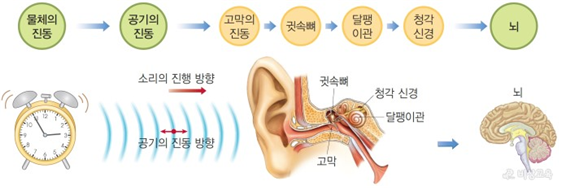
소리의 특징
소리는 기본적으로 주파수(frequency)와 진폭(amplitude)을 가지는데, 주파수는 단위 시간 내에 몇 개의 주기나 파형이 반복되었는가를 나타내는 수를 말하며, 진폭은 주기적인 진동이 있을 때 진동의 중심으로부터 최대로 움직인 거리 혹은 변위를 뜻합니다.
파동(wave)은 반복적으로 진동하는 신호를 나타내기 때문에 우리는 소리를 waveform 형태로 나타낼 수 있습니다.

위의 그래프에서 진폭(amplitude)은 파동(wave)의 최대값을 나타내며, 특정 지점에서 반복적으로 나타나는 어떠한 지점이 있을 떄 cycle이 있다고 하며 cycle 1회가 걸리는 시간을 주기(period or wavelength)라고 합니다.
이를 확장시켜 주파수(frequency)로 1초에 몇 번 cycle이 반복되는지(cycles per second)를 가라킵니다. 보통 cycles per second를 헤르츠(hertz, 줄여서 Hz)라고 표기합니다.
위의 그래프에 대입시켜보면 4개의 cycle이 존재하며, 1개의 cycle은 대략 0.25초의 주기로 나타나고 있습니다. 따라서 1초까지 cycle이 4회 반복되었으므로 이 파동의 주파수는 즉 4Hz입니다.
이를 통해 주기 $T$와 주파수 $f$ 사이에는 다음과 같은 관계를 가지고 있음을 알 수 있습니다. \(T=\frac { 1 }{ f }\)
Analog Digital Conversion
아날로그는 기본적으로 신호나 자료를 연속적인 물리량으로 나타낸 것이기 떄문에 컴퓨터가 이러한 신호를 이해하기 위해서는 디지털 신호로 변환시켜주어야 합니다. 이러한 과정은 2 step으로 이루어지게 됩니다.
Sampling
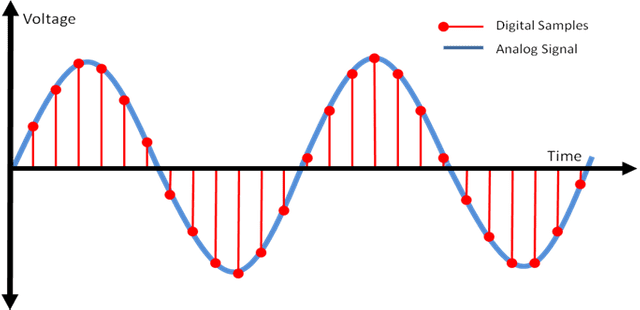
일정한 시간 간격마다 음성 신호를 샘플해서 연속 신호(continous signal)을 이산 신호(discrete signal)로 변환합니다. 이때 1초에 몇 번 샘플하는지를 나타내는 지표가 바로 sampling rate입니다. 예를 들어, Sample rate = 44100Hz인 소리의 경우 1초에 44100개의 sample을 추출하였다는 말입니다.
Quantization
다음으로는 샘플링 된 신호에 양자화(quantization)을 실시하는 과정입니다. 양자화란 실수 범위의 이산 신호를 정수 범위의 이산 신호로 바꾸는 걸 의미합니다. 만약 8비트 양자화를 실시한다면 실수 범위의 이산 신호가 -128~127의 정수로, 16비트 양자화를 한다면 실수 범위의 이산 신호가 -32768~32767 정수로 변환됩니다. 양자화 비트 수(Quantization Bit Depth)가 커질 수록 원래 음성 신호의 정보 손실을 줄일 수 있지만 그만큼 저장 공간이 늘어나는 단점이 있습니다.
Fourier Transform
푸리에 변환은 임의의 입력 신호를 다양한 주파수를 갖는 주기함수들의 합으로 분해하여 표현하는 것으로 시간(time)에 대한 함수(혹은 신호)와 주파수(frequency)에 대한 함수(혹은 신호)를 잇는 수학적인 연산을 가리킵니다.
푸리에 변환에 대한 자세한 설명은 3blue1brown의 동영상을 참고 부탁드립니다.
푸리에 변환의 역할은 어떠한 waveform을 time domain에서 frequency domain으로 변환시키는 것입니다. 이를 사용하는 근본적인 이유는 time domain에서 해석하기 힘든 신호를 frequency domain에서 쉽게 해석할 수 있기 때문입니다.
아무튼 이렇게 푸리에 변환을 통과해, time domain에서 frequency domain으로 바뀐 그래프를 스펙트럼(Spectrum) 이라고 정의합니다. 스펙트럼은 기존의 waveform과는 아래와 같이 다른 의미를 나타내게 됩니다.
- x_axis: time -> frequency
- y_axis: amplitude -> mangnitude
푸리에 변환을 실제로 적용할 때는 고속 푸리에 변환(Fast Fourier Transform)이라는 기법을 씁니다. 기존 푸리에 변환에서 중복된 계산량을 줄이는 방법입니다.
Difference magnitude and amplitude
signal domain에서 magnitude와 amplitude는 모두 진폭으로 해석되는데 이 두 용어에 대한 차이를 이해하는 것이 중요하다. 앞서 amplitude는 파동(wave)의 최대값을 나타낸다고 하였는데 사실 이는 반만 맞는 말이다. 정확하게는 중심 위치(time=0)에서부터 양수 또는 음수값까지의 편차를 측정한 값이라고 할 수 있다. 따라서 amplitude는 방향을 고려한 vector로 time domain에서 주로 사용된다.
하지만 magnitude는 방향에 관계없이 값이 0과 얼마나 다른지를 측정한다. 따라서 크기는 항상 양수를 가지며 방향을 고려하지 않기 때문에 scalar로 frequency domain에서 주로 사용 한다.
두 용어에 대한 의미를 통해서 amplitude에 절대값을 씌우면 magnitude를 구할 수 있는 것은 당연해보인다. 따라서 frequency domain에서 magnitude를 사용하는 근본적인 이유는 푸리에 변환을 통한 통한 분리된 각 frequency가 전체 소리에 얼마나 영향을 주는지 정도를 나타내기 위함이다.
Spectrogram
위에서 푸리에 변환을 통해 얻은 스펙트럼(Spectrum)은 시간 정보가 없어지게 되는데, 따라서 시간 정보를 보존해주기 위해 Short Time Fourier Transfrom(STFT) 라는 푸리에 변환 방법을 사용한다.
STFT는 파형(waveform)을 일정한 특정 길이의 frame으로 잘라서 각 frame마다 푸리에 변환을 취하고, 스펙트럼(Spectrum)을 구하는 방법을 취한다. 이렇게 음성 전체로부터 얻은 여러 개의 스펙트럼(Spectrum)을 시간 축에 나열하면 시간 변화에 따른 스펙트럼의 변화를 스펙트로그 (Spectrogram) 으로 정의한다.
스펙트로그램(Spectrogram)은 소리나 파동을 시각화하여 파악하기 위한 도구로, 파형(waveform)과 스펙트럼(spectrum)의 특징이 조합되어 있다.
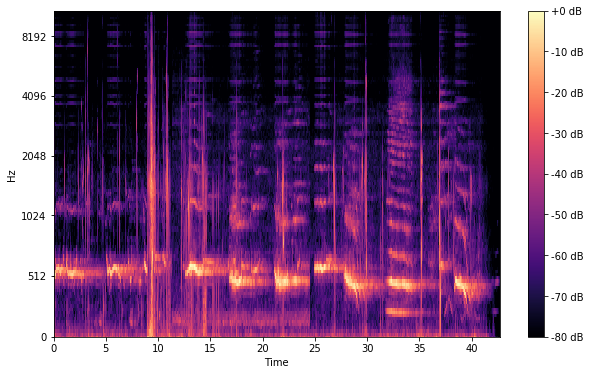
파형(waveform)에서는 시간(time)축의 변화에 따른 진폭(amplitude) 축의 변화를 볼 수 있고, 스펙트럼(Spectrum)에서는 주파수(frequency)축의 변화에 따른 진폭(magnitude) 축의 변화를 볼 수 있는 반면, 스펙트로그램(Spectrogram)에서는 시간축과 주파수 축의 변화에 따라 진폭의 차이 또는 이를 dB로 변환하여 색으로 표현합니다.
Power, dB
$k$ 번째 주파수 구간(bin)에 해당하는 푸리에 변환 결과를 $X[k]$라고 할 때 파워(Power)를 구하는 공식은 아래와 같습니다.
\[\text{Power}=\frac { { \left| X\left[ k \right] \right| }^{ 2 } }{ N }\]$N$은
NFFT로 푸리에 변환을 통해서 주파수 도메인으로 변환할 때 몇 개의 구간(bin)으로 분석할지를 나타냅니다.
쉽게 생각하면 진폭(magnitude)을 제곱한 것이 파워(Power)라고 볼 수 있습니다.
데시벨(dB)은 로그값을 부르는 단위로 어떠한 값 $x$에 대해 $10 * log{x}$로 나타낸 값을 표현합니다. 왜 사용하는 것일까요? 각기 다른 음압(sound pressure)을 가지는 소리들을 예시로 살펴보겠습니다.
- 1v(0dB) -> 2v(3dB)
- 100v(20dB) -> 200v(23dB)
dB는 어떤 숫자간의 곱의 관계를 나타내는 상대적인 의미의 값이기 때문에 위의 경우 어떤 신호가 2배가 된다는 것은 dB 스케일에서는 +3dB를 의미합니다. 일반적으로 사람의 귀는 예민하지 않다면 1dB의 변화를 잘 감지하지 못한다고 합니다.
즉 주파수(frequency)를 가지는 신호의 성질은 dB 스케일에 정량적으로 비례하는 특성을 가지고 있다는 점입니다. 따라서 주파수(frequency)는 magnitude(진폭)보다 그것의 지수를 취한 log 스케일에 비례하는 특성을 가지며, 그것을 개념적으로 쉽게 표현하기 위해 dB 스케일을 사용합니다.
Mel-Scale
Mel-scale은 실제 주파수 정보를 인간의 청각 구조를 반영하여 수학적으로 변환하기 위한 대표적인 방법입니다.
사람의 청각기관은 고주파(high frequency) 보다 저주파(low frequency) 대역에서 더 민감하다고 합니다. 이러한 이유를 달팽이관의 구조로 살펴보면 달팽이관의 가장 안쪽 청각 세포는 저주파 대역을 인지하며, 바깥쪽 청각 세포는 고주파 대역을 인지한다는 사실을 통해 모든 주파수 대역을 같은 비중으로 인지하지 않고, 고주파에서 저주파로 내려갈수록 담당하는 주파수 대역이 점점 더 조밀해진다는 점입니다.
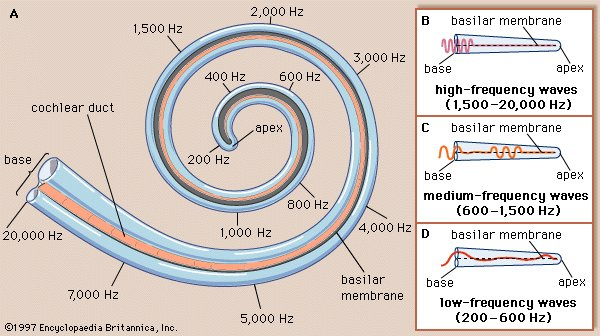
이러한 달팽이관의 특성에 맞춰서 물리적인 주파수와 실제 사람이 인식하는 주파수의 관계를 표현한 것이 Mel-scale이라 합니다.
Mel-scale은 Filter-Bank 기법을 통해 수행되어 집니다. Mel-Scale은 Filter Bank를 나눌 때 어떤 간격으로 나눠야 하는지 알려주는 역할을 합니다.
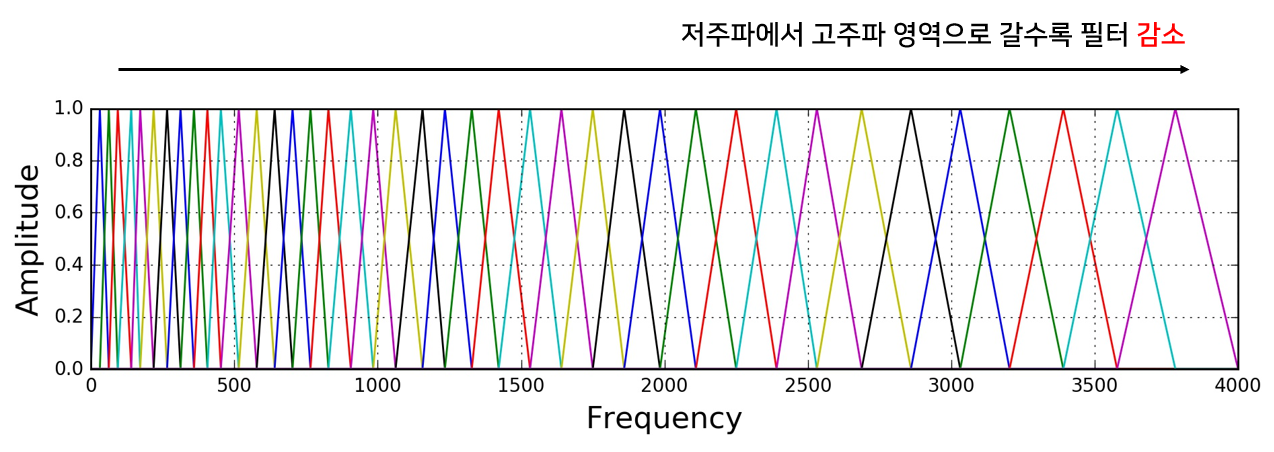
앞서 언급했듯이 달팽이관의 특성을 고려해서 낮은 주파수에서는 세밀하기 살피기 위해서 촘촘한 삼각형 Filter를 가지고, 고주파 대역으로 갈수록 넓은 삼각형 Filter를 가지게 됩니다.
이 Mel Scale에 기반한 Filter Bank를 Spectrum에 적용하여 도출해낸 것이 Mel Spectrum입니다.
Reference
[Sound AI #10] 오디오 데이터 전처리 (이론)
Comments