5 min to read

힙(Heap)이란?

Concept

Featured image

Table of Contents

정의

힙이란 데이터에서 최소값과 최대값을 빠르게 찾기 위해 고안된 완전 이진트리 형태의 자료구조를 말합니다. 즉 우선 순위 큐를 위하여 만들어진 자료구조입니다.

완전 이진트리는 마지막 레벨을 제외 하고 모든 레벨이 완전히 채워져 있는 이진트리의 구조입니다. 마지막 레벨의 경우, 꽉 채워져 있을 필요는 없지만 노드가 왼쪽에서 오른쪽으로 채워져있어야 합니다.

우선순위 큐란?

스택과 큐

스택(Stack)은 말 그대로 데이터를 차곡차곡 쌓아 올린 형태의 자료구조이며, 입출력의 경로가 한 곳으로 지정된 경우를 말합니다.

따라서 아래 그림과 같이 데이터가 순서대로 쌓이며, 가장 마지막에 삽입된 데이터가 가장 먼저 삭제되는 구조를 가지고 있습니다. 보통 이러한 구조를 후입선출 또는 LIFO(Last IN First Out)이라고 합니다.

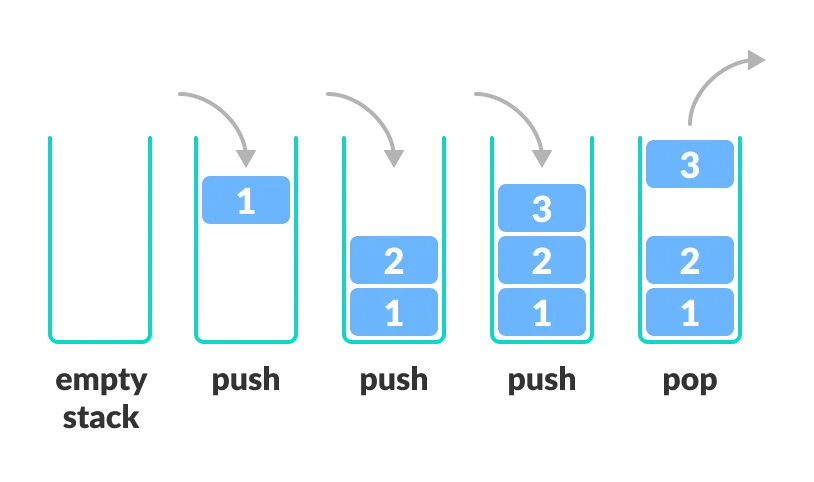
image

그림에서 볼 수 있듯이, 스택에서는 데이터의 삽입과 삭제를 push와 pop 연산을 통해 수행합니다.

큐(Queue)는 스택과 다르게 입출력의 경로를 다르게 지정한 경우를 말합니다. 즉 데이터의 삽입과 삭제가 처리되는 경로가 따로 존재합니다.

큐의 가장 첫 원소를 front, 끝 원소를 rear라고 지칭하며, 들어올 때 rear로 들어오지만, 나올 때는 front부터 빠지는 특성을 가집니다. 즉 선입선출 또는 FIFO(First In First Out) 구조를 가집니다.

또한 큐의 rear에서 이루어지는 삽입연산을 enQueue, front에서 이루어지는 삭제연산을 deQueue라고 부릅니다.

image

우선순위 큐

일반적인 큐와 다르게 우선순위 큐에서는 front가 아니라 아래의 그림처럼 우선순위가 높은 데이터가 가장 먼저 나오게 되는 차이점이 있습니다.

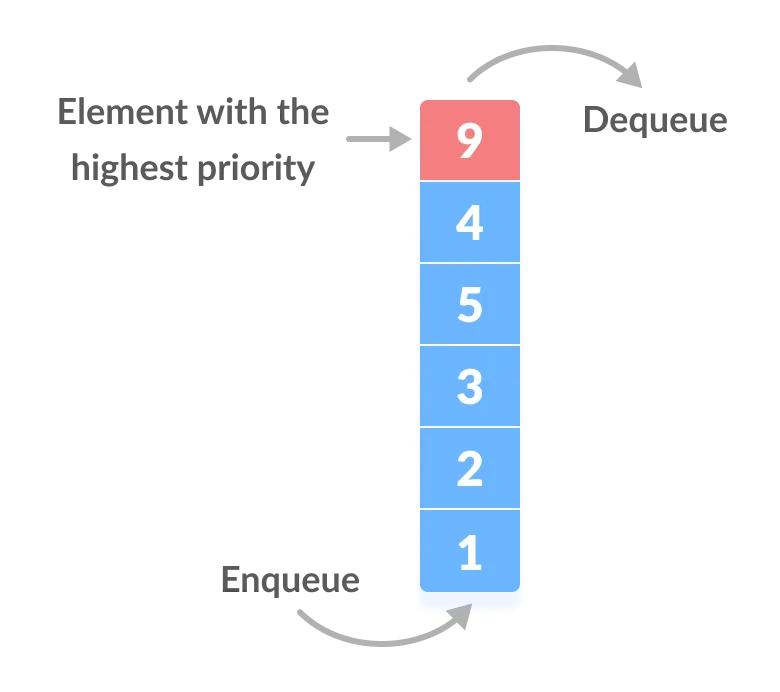
image

우선순위 큐는 배열, 연결리스트, 힙으로도 구현이 가능하지만 이 중에서 힙으로 구현하는 것이 가장 효율적입니다.

Operations peek insert delete
Array O(1) O(1) O(n)
Linked List O(1) O(n) O(1)
Heap O(1) O(log n) O(log n)

특징

힙은 완전 이진트리 형태의 구조를 가지지만, 구별되는 몇 가지 특징들이 있습니다.

종류

힙은 최소값과 최대값을 빠르게 찾기 위해 고안된 형태이므로, 목적에 따라 힙의 종류도 구분됩니다.

최대 힙(Max Heap)

부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 형태를 가집니다.

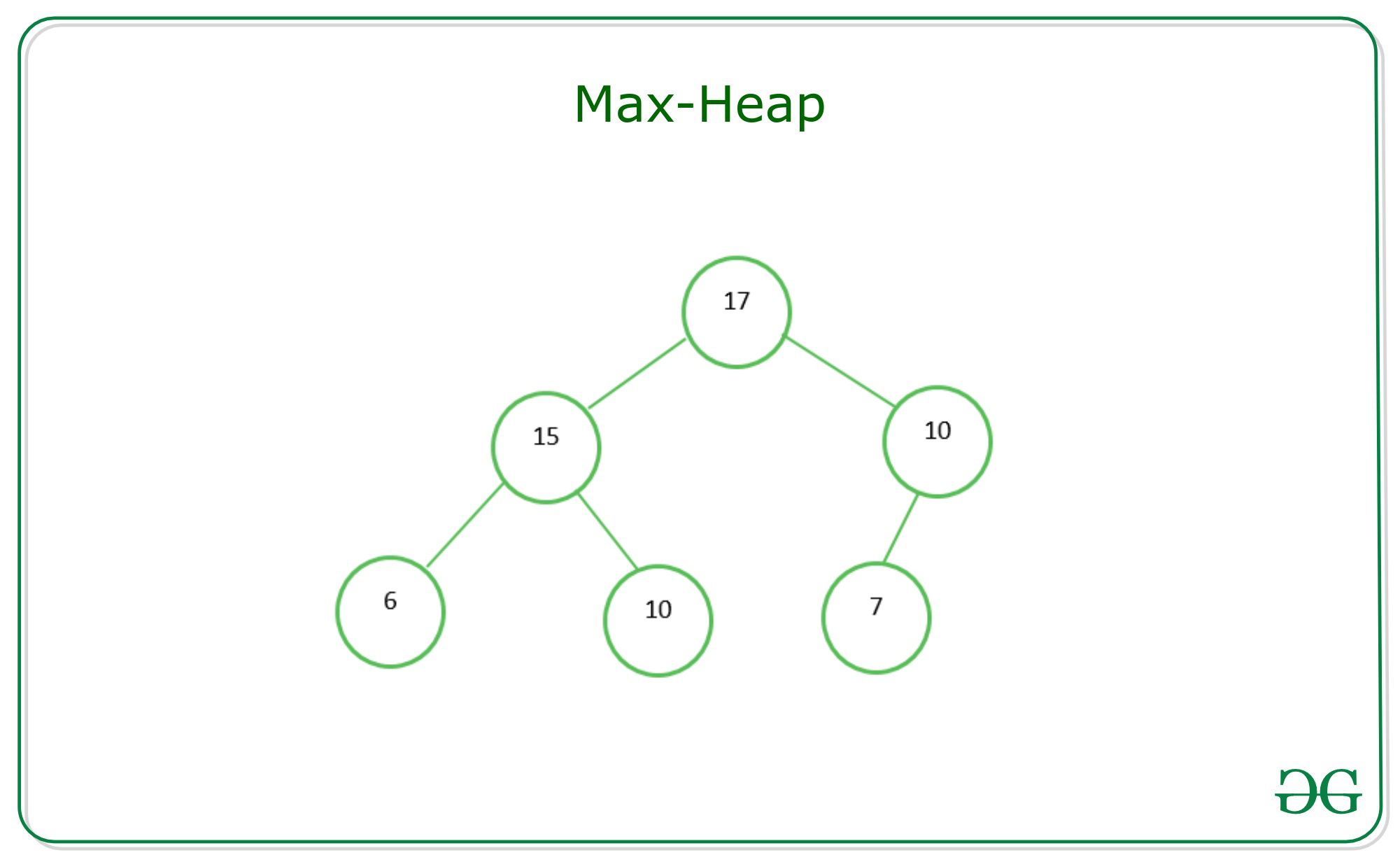
image

최소 힙(Min Heap)

부모 노드의 키 값이 자식 노드의 키 값보다 항상 작은 형태를 가집니다.

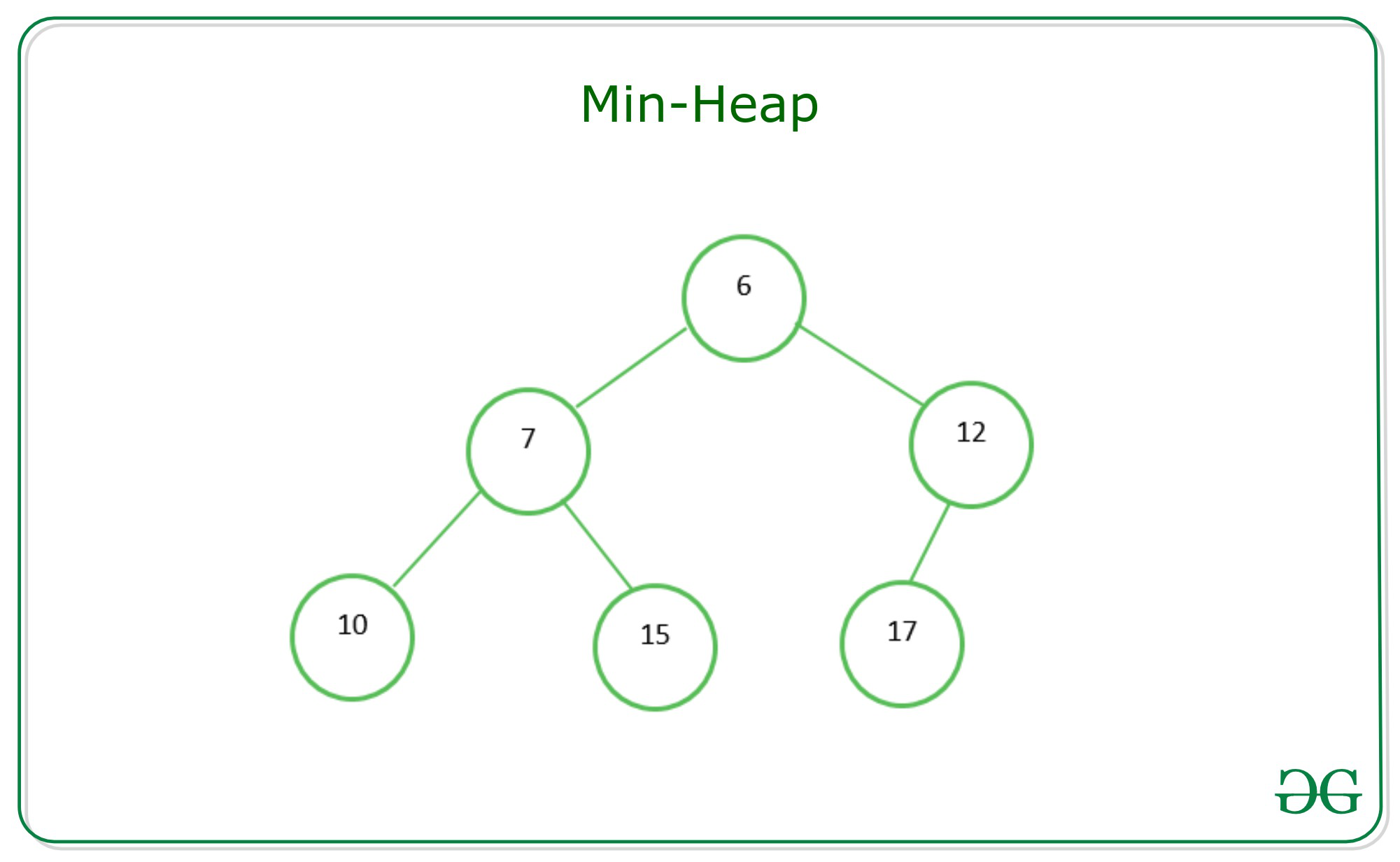
image

구현

힙은 완전 이진트리 성질을 만족하기 때문에 다음처럼 1차원 배열(array)로도 표현이 가능합니다.

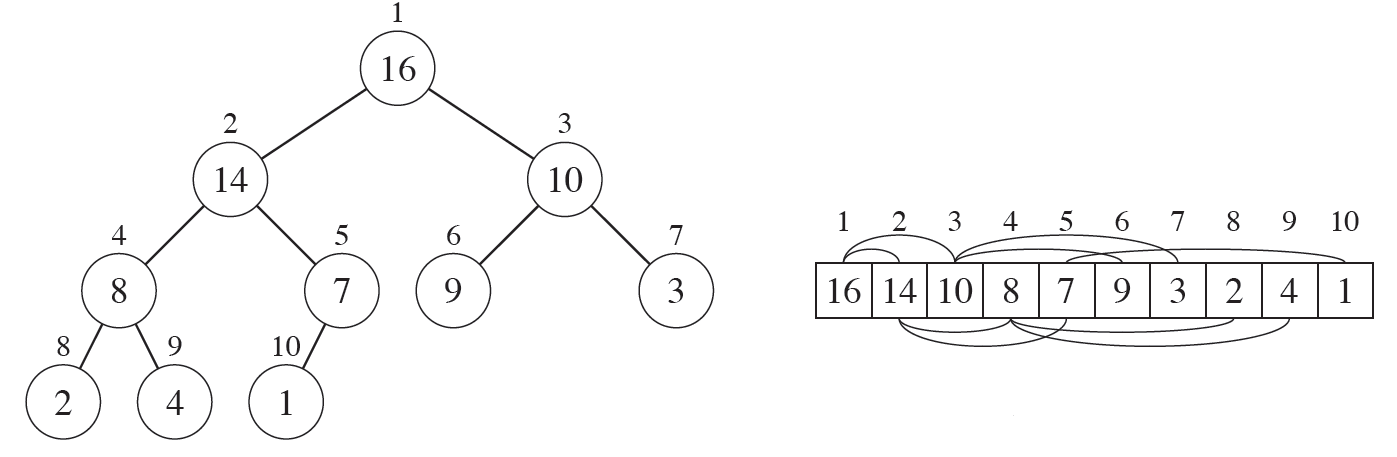
image

눈에 띄는 것은 파이썬의 인덱스는 0번부터 시작하지만, 구현을 쉽게 하기 위하여 첫번째 인덱스를 1번부터 시작하게 됩니다. 즉 특정 위치의 노드 인덱스는 새로운 노드가 추가되어도 변하지 않게 됩니다.(e.g. 루트 노드의 오른쪽 노드의 인덱스는 항상 3입니다.)

따라서 노드의 인덱스는 아래와 같은 관계를 가지게 됩니다.

heap in Python

파이썬에서는 내장된 heapq 모듈을 사용하여 최소/최대 힙을 구현할 수 있습니다.

heapq 모듈은 리스트를 최소 힙처럼 다룰 수 있도록 하기 때문에, 빈 리스트를 생성한 후 heapq의 함수를 호출할 때마다 리스트를 인자에 넘겨야 합니다. 다만 이미 생성해둔 리스트가 있다면, heapify 함수를 통해 즉각적으로 힙 자료형으로 변환할 수 있습니다.

import heapq

heap = []
heapq.heapqush(heap, 4)
heapq.heappush(heap, 3)
heapq.heappush(heap, 2)
heapq.heappush(heap, 1)

print(heap) # [1, 3, 2, 4]

# 리스트가 주어진 경우
arr = [4, 3, 2, 1]
heapq.heapify(arr)

print(arr) # [1, 3, 2, 4]

최소값을 나타내기 위해서는 인덱싱을 통해 접근하거나, pop을 사용하여 가져올 수 있습니다.

# 인덱싱을 통한 접근
minVal = arr[0]

print(minVal) # minVal = 0

# pop 메서드를 이용
res = heapq.heappop(arr)

print(res) # 1
print(arr) # [2, 3, 4]

heapq에서 최대 힙을 제공하지는 않기 때문에 최대 힙을 구현하기 위해서는 약간의 트릭이 필요합니다.

트릭은 힙에 원소를 추가할 때 (-value, value)의 튜플 형태로 넣어주면, 튜플의 첫 번째 원소를 우선순위로 힙을 구성하게 됩니다. 이때 원소 값의 부호를 바꿨기 때문에, 최소 힙으로 구현된 heapq 모듈을 최대 힙 구현에 활용할 수 있습니다.

arr = [1,3,5,7,9]

max_heap = []
for i in arr:
  heapq.heappush(max_heap, (-i, i))

print(max_heap) # [(-9, 9), (-7, 7), (-3, 3), (-1, 1), (-5, 5)]

최대값을 나타내기 위해서는 최소 힙에서 구현된 방식과 유사하지만, 추가로 튜플 내에서 인덱싱이 필요합니다.

# 인덱싱을 통한 접근
maxVal = max_heap[0][-1]

print(minVal) # maxVal = 9

# pop 메서드를 이용
res = heapq.heappop(arr)

print(res) # (-9, 9)
print(res[-1]) # 9

Reference

https://www.programiz.com/dsa/stack/

https://www.geeksforgeeks.org/difference-between-min-heap-and-max-heap/

https://ratsgo.github.io/data%20structure&algorithm/2017/09/27/heapsort/