5 min to read

What is Odds, Logit and Sigmoid?

Research

Featured image

Table of Contents

Odds, Logit, Sigmoid

Bayes Theorem

베이즈 정리는 불확실성 하에서 의사결정 문제를 수학적으로 다룰 때 사용하는 것으로 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 수식입니다. 공식은 아래와 같습니다.

\[P(Y|X) = \frac{P(X|Y)P(Y)}{P(X)}\]

$P(Y \mid X)$: 사후확률(posterior probability)

$P(X \mid Y)$: 가능도(likelihood)

$P(Y)$: 확률변수 Y의 사전확률(prior probability)

$P(X)$: 확률변수 X의 사전확률(prior probability) == Evidence

Classification 문제를 가정하였을떄, X를 Data, Y를 Class로 생각해보겠습니다.

\(P(X \mid Y)\)는 각 Class에 속해 있는 Data의 확률 분포(Prior),

\(P(Y \mid X)\)는 새로운 데이터가 들어 왔을 경우 Y의 분포(Posterior)

확률의 Marginal 특징에 의하여 분모인 Evidence는 다음과 같이 쓸 수 있습니다.

\[P(X) = \sum _{j}^{}{P(X|Y_j) P(Y_j)}\]

우리가 분류를 하고자 할 때, 즉 새로운 데이터를 분류하고자 할 때 사후확률을 기준으로 삼게 됩니다.

\[\begin{array}{l} X: Y_{1} \text { if } P\left(Y_{1} \mid X\right)>P\left(Y_{2} \mid X\right) \\ \\ X: Y_{2} \text { if } P\left(Y_{1} \mid X\right)<P\left(Y_{2} \mid X\right) \end{array}\]

위와 같이 $Y_{1}$과 $Y_{2}$ 두개의 Class가 있을 경우에 판별 기준인 Posterior를 전개해 보도록 하겠습니다.

\[\begin{aligned} P\left(Y_{1} \mid X\right) &=\frac{P\left(X \mid Y_{1}\right) P\left(Y_{1}\right)}{P(X)} \\ \\ P\left(Y_{2} \mid X\right) &=\frac{P\left(X \mid Y_{2}\right) P\left(Y_{2}\right)}{P(X)} \end{aligned}\]

그런데 여기서 분모는 $P(X)=P\left(X \mid Y_{1}\right) P\left(Y_{1}\right)+P\left(X \mid Y_{2}\right) P\left(Y_{2}\right)$ 이므로 두 식에서 모두 같습니다.

즉 Posterior, 사후 확률은 Likelihood와 Prior의 곱이 결정한다는 것입니다.

Logit, Odds

우리가 하고자 하는 것은 $X$가 어떤 클래스일지 맞추는 간단한 문제를 해결하는 것입니다. 위와 같이, 우리는 간단하게 사후확률을 기준으로 $P(Y_1 | X)$와 $P(Y_2 | X)$중 큰 값을 $X$의 클래스로 예측하면 됩니다.

좀 더 간단하게 Posterior를 전개하는 대신, 확률의 비인 Odds를 이용해서 표현할 수 있습니다. Odds(승산)이란 임의의 사건 A가 발생하지 않을 확률 대비 일어날 확률의 비율을 뜻하는 개념입니다.

즉, Odds가 클수록 성공확률이 크다는 의미입니다. 따라서 아래와 같은 식으로 쓸 수가 있습니다.

\[odds=\frac { P(A) }{ P({ A }^{ c }) } =\frac { P(A) }{ 1-P(A) }\] \[\text {Choose}=\left\{\begin{array}{ll}A & \text { if } \:odds>1 \\A^c & \text { if } \:odds<1 \end{array}\right.\]

만약 $P(A)$가 1에 가까울 수록 승산은 치솟을 겁니다. 반대로 $P(A)$가 0이라면 0이 될 겁니다. 바꿔 말하면 승산이 커질수록 사건 $A$가 발생할 확률이 커진다고 이해해도 될 겁니다.

$P(A)$를 $x$축, 사건 $A$의 승산을 $y$축에 놓고 그래프를 그리면 아래와 같습니다.

\[0<odds<\infty\]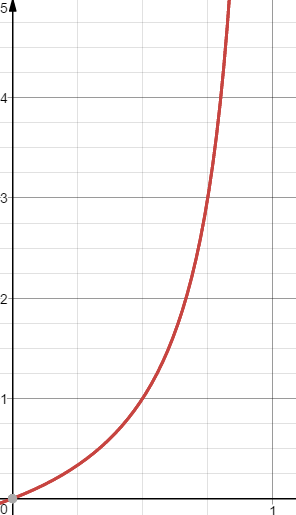

Untitled

다시 처음 문제로 돌아와서 생각을 합시다.

\[P(Y=1 \mid X=\vec{x})=\beta_{0}+\beta_{1} x_{1}+\beta_{2} x_{2}+\ldots+\beta_{p} x_{p}\]

위 식에서 좌변의 범위는 확률로 0~1 사이입니다. 하지만 우변은 음의 무한대에서 양의 무한대 범위를 가지기 때문에 식이 성립하지 않는 경우가 존재할 수 있습니다. 여기서 식을 한번 더 바꿔서, 좌변을 승산(odds)으로 설정해 보겠습니다. 아래 식처럼 쓸 수 있습니다.

\[\frac{P(Y=1 \mid X=\vec{x})}{1-P(Y=1 \mid X=\vec{x})}=\beta_{0}+\beta_{1} x_{1}+\beta_{2} x_{2}+\ldots+\beta_{p} x_{p}\]

좌변(승산)의 범위는 0에서 무한대의 범위를 갖습니다. 하지만 우변(회귀식)은 그대로 음의 무한대에서 양의 무한대 범위입니다.

이 떄, log를 odds에다가 붙여서 logit이라는 것을 정의합니다. odds에다가 log를 취하면 logit이 됩니다.

log 변환은 통계학에서 자주 사용하는 변환으로 다음과 같은 장점을 지닙니다.

logit의 그래프는 아래와 같습니다.

\[-\infty<logit<\infty\]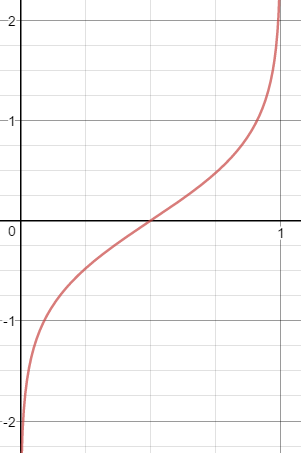

Untitled 1

이렇게 되면 logit의 범위 또한 우변처럼 음의 무한대에서 양의 무한대가 됩니다. 이제야 비로소 좌변(logit)이 우변(회귀식)의 범위와 일치하게 됩니다.

\[\begin{aligned}\operatorname{logit} &=\log (\text {odds}) \\ \\ &=\log \left(\frac{y}{1-y}\right) \\ \\ &=\log \left(\frac{P\left(Y_{1} \mid X=\vec{x}\right)}{1-P\left(Y_{1} \mid X=\vec{x}\right)}\right)\end{aligned}\]

Logistic Function (a.k.a Sigmoid Function)

\[y=\frac { 1 }{ 1+{ e }^{ -x } }\]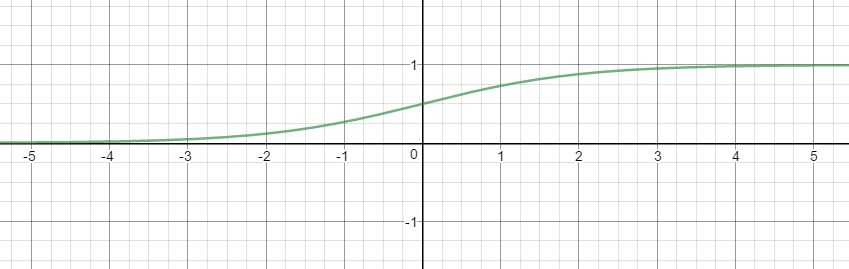

Untitled 2

logistic 함수는 위의 그래프와 같이 $x$값으로 실수 전체를 받을 수가 있지만, 출력 결과는 항상 0에서 1사이 값이 됩니다.

위에서 우리는 \(P(Y_{1} \mid X)\)를 알기 위해 좌변에 logit함수를 적용하여, 음의 무한대에서 양의 무한대로 범위를 맞춰주었습니다. logistic 함수가 실수 전체를 받을 수 있다면, logit함수의 결과에 logistic 함수를 적용하여 0에서 1사이 값의 확률로 $P(Y_1 | X)$를 나타낼 수 있습니다.

\[\operatorname{logit}(y)=\log _{e}\left(\frac{y}{1-y}\right)=z\] \[\begin{array}{l} =\frac{y}{1-y}=\exp (z) \\ \\ =\frac{1}{y}-1=\frac{1}{\exp (z)} \\ \\ =\frac{1}{y}=\frac{1+\exp (z)}{\exp (z)} \\ \\ =y=\frac{\exp (z)}{1+\exp (z)} \\ \\ =y=\frac{1}{1+\exp (-z)} \\ \\ =\operatorname{sigmoid}(z) \end{array}\]

이러한 logit함수와 logistic(sigmoid) 함수는 서로 역함수 관계입니다.

Code Pratice

import numpy as np

def odds(p):
    """성공확률 / 실패확률"""
    return p / (1 - p)

def logit(p):
    """odds에 log를 취한 값"""
    return np.log(odds(p))

def sigmoid(z):
    """logistic:
    logit(odds에 log를 취한 값)을 알고 있을 때, 성공 확률 p를 계산"""
    return 1 / (1 + np.exp(-z))

확률 p는 logit함수와 sigmoid함수를 통과한 probability와 동일합니다.

p = 0.8
print(f'p = {p}, odds(p) = {odds(p)}, logit(p) = {logit(p)}')
# p = 0.8, odds(p) = 4.000000000000001, logit(p) = 1.3862943611198908

z = logit(p)
probability = sigmoid(z)
print(f'probability={probability}')
# probability=0.8

logistic 회귀의 결과가 실제로 sigmoid함수를 통해 나오는지를 확인해보겠습니다.

from sklearn.linear_model import LogisticRegression

X = np.random.randn(10,3)
y = np.random.randint(2, size=10)

clf = LogisticRegression.fit(X, y)

proba = np.round(clf.predict_proba(X[:, :]),2)
# proba is array([[0.24, 0.76], [0.88, 0.12], [0.68, 0.32], [0.79, 0.21], [0.4 , 0.6 ], [0.07, 0.93], [0.36, 0.64], [0.69, 0.31], [0.42, 0.58], [0.48, 0.52]])

coef = np.array(clf.coef_)
coef = coef.reshape(-1,1)

# Broadcasting
pred = np.dot(X, coef)+clf.intercept_

np.round(sigmoid(pred),2)
# array([[0.76], [0.12], [0.32], [0.21], [0.6 ], [0.93], [0.64], [0.31], [0.58], [0.52]])

Next

Reference

logit, sigmoid, softmax의 관계

Bayes Theorem과 Sigmoid와 Softmax사이의 관계

logistic 회귀