5 min to read

Understanding Metric Learning, Chapter1

Research

Featured image

Table of Contents

Understanding Metric Learning, Chapter1

머신 러닝에서 분류와 회귀등의 문제를 해결하기 위해서는 주어진 데이터로부터 특징을 잘 파악하는 것이 중요합니다. 이러한 특징을 잘 파악하기 위해서 우리는 도메인 지식을 학습하고, Task에 맞게 전처리를 수행합니다. Metric Learning은 특징간의 거리를 학습하는 것을 목표로 하면서 특징을 파악하기 위한 방법 중 하나입니다.

머신 러닝에서 이러한 거리를 사용하는 방법은 사실 이전부터 존재해왔습니다. 전통적인 군집분석이나 K-NN등의 방법이 예시로 사용될 수 있습니다. 이러한 거리 기반의 학습방법은 모두 공통된 특징을 갖고 있습니다. 바로 유사도 즉 ‘Similarity’를 기반으로 학습한다는 것이었습니다.

Metric Learning은 유사한 특징간에는 거리를 가깝게 학습하고, 유사하지 않다면 거리를 멀어지도록 학습합니다.

당연하게 특징간의 거리를 비교하기 때문에 특징을 잘 표현하는 것은 중요한 문제입니다. 데이터가 이미지나 자연어와 같은 비정형데이터로 이루어져, 고차원을 가지는 데이터라면 어떻게 특징을 표현할 수 있을까요?

위에서 언급한 전통적인 방법들은 고차원의 데이터를 표현하기에는 하드웨어적 성능이 부족하다는 한계점을 지니게 됩니다. 데이터의 차원이 증가하면서, 표현되는 데이터의 양은 기하급수적으로 증가하면서 차원의 저주에 빠지게 됩니다. 이러한 문제를 해결하기 위해 딥러닝을 이용하여 문제 해결을 시도하게 되었습니다.

Invariant Scattering Convolution Networks의 논문에서 ‘CNN은 차원의 저주를 극복하고 이미지 데이터에 내재된 불변량(invariant)을 찾아낸다’라는 추측을 수학적으로 참인 명제로 증명해내었습니다.

물론 딥러닝도 차원의 저주 문제를 완전히 해결할 수는 없지만 기존의 Metric Learning은 딥러닝을 이용하여 특징을 찾아 거리를 학습하는 방식인 Deep Metric Learning으로 발전하게 됩니다.

최근에는 얼굴 인식 분야에서 Metric Learning이 얼굴 인식에서 상당히 많은 연구가 진척되고 활용되고 있습니다. 얼굴 인식과 같은 이미지 분야의 데이터에서 가장 어려운 것은 유사한 데이터 간 서로 다른 특징을 가지는 데이터간의 분류입니다. 아래는 강아지 쉽독과 대걸레의 이미지입니다.

Untitled

두 이미지는 서로 다른 이미지가 분명함에도, 사람이 봐도 구분이 어려울 정도로 유사합니다. Metric Learning은 이러한 이미지들의 구분이 잘 되도록, 특징을 학습할 수 있다는 장점이 있습니다.

또한 이미지 뿐만 아니라, 검색과 추천등의 분야에서도 Query의 결과들을 Rank로 나타내기 위해서 Metric Learning을 활용합니다. 따라서 Metric Learning은 Ranking Loss로 불리기도 합니다.

Loss in Metric Learning

위에서 metric learning은 유사한 특징간에는 거리를 가깝게 학습하고, 유사하지 않다면 거리를 멀어지도록 학습시킨다고 말씀드렸습니다. 사실 개념 자체는 간단하기 때문에 metric learning은 거리를 잘 학습할 수 있도록,네트워크 구조보다는 효과적인 loss를 계산하도록 발전되어왔습니다.

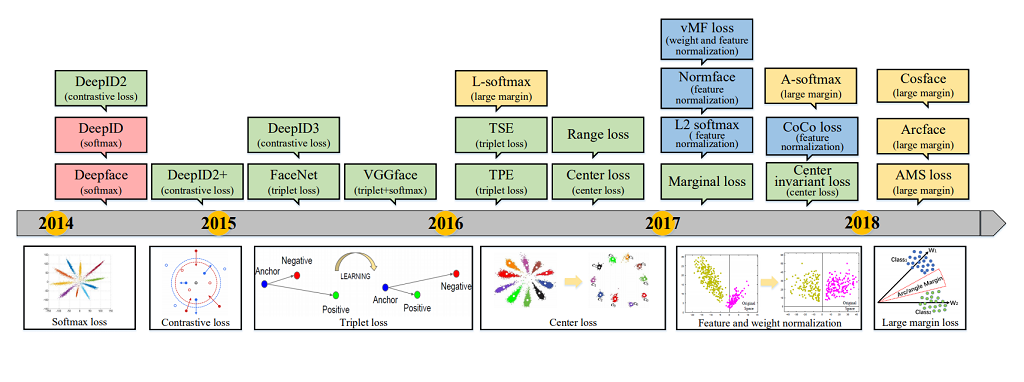Untitled 1Source: https://arxiv.org/pdf/1804.06655.pdf

이 글에서는 대표적으로 Pairwise Loss, Triplet Loss의 방법을 살펴보겠습니다. 아래의 방법들에서 metric은 모두 Euclidean 거리 를 기반으로 합니다.

Pairwise Loss

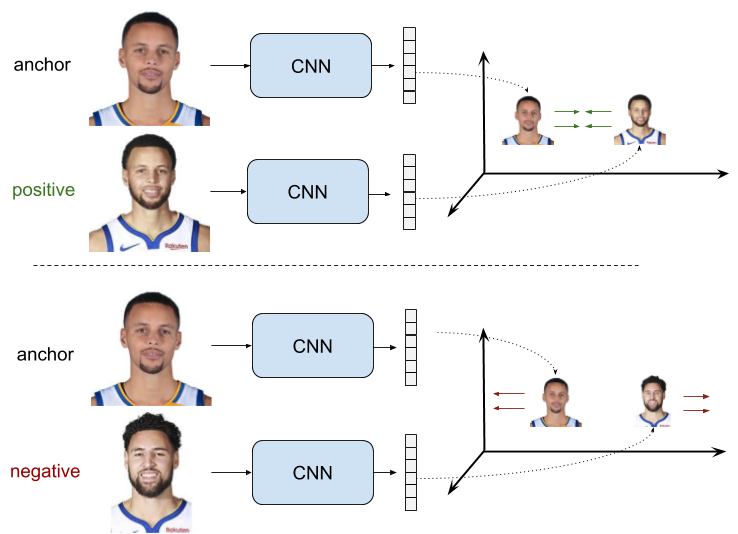
Untitled 2

Pairwise loss는 유사한 특징 간에는 거리를 0이 되도록 학습하고, 유사하지 않다면 설정한 margin보다 크게 거리를 학습하도록 합니다. margin의 효과는 이는 유사하지 않은 특징간의 거리가 이미 충분히 멀다면,
무시하고 어려운 특징 쌍을 학습하는데 집중합니다.

\[L\left(r_{0}, r_{1}, y\right)=y\left\|r_{0}-r_{1}\right\|+(1-y) \max \left(0, m-\left\|r_{0}-r_{1}\right\|\right)\]

$r_{0}$ and $r_{1}$ are the pair elements representations

$y$ is a binary flag,

$m$ is margin

구현 코드는 아래와 같습니다.

class MarginRankingLoss(nn.Module):
    def __init__(self, margin=0., size_average=True):
        super(MarginRankingLoss, self).__init__()
        self.margin = margin

    def forward(self, input1, input2, target):
        losses = F.margin_ranking_loss(input1, input2, target, margin=self.margin)
        return losses.mean() if size_average else losses.sum()

Triplet Loss

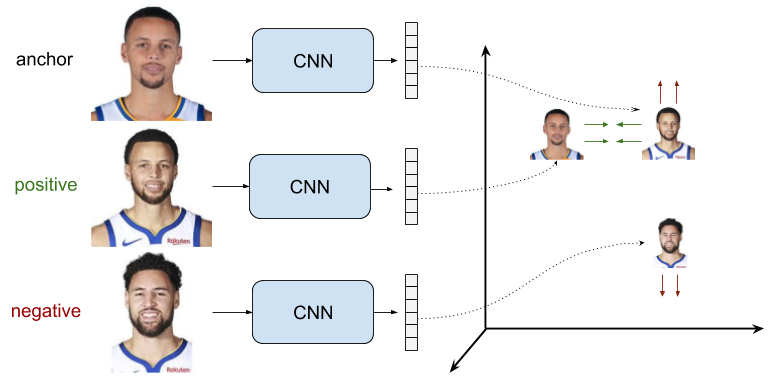
Untitled 3

이전과 유사하지만 anchor, positive, negative의 입력 구조를 가지면서, anchor와 positive가 가깝게하면서 anchor와 negative는 멀게하도록 학습합니다 세 개의 특징 사이의 관계를 고려하기 때문에 좀 더 유연하면서 성능적으로 우수합니다.

\[L\left(r_{a}, r_{p}, r_{n}\right)=\max \left(0, m+d\left(r_{a}, r_{p}\right)-d\left(r_{a}, r_{n}\right)\right)\]

$r_{a}$: anchor representation

$r_{p}$: a positive representation

$r_{n}$: a negative representation

$d$: euclidean distance

$m$: margin

loss는 3가지의 상황으로 분류 될 수 있습니다.

그림으로 나타내면 아래와 같습니다.

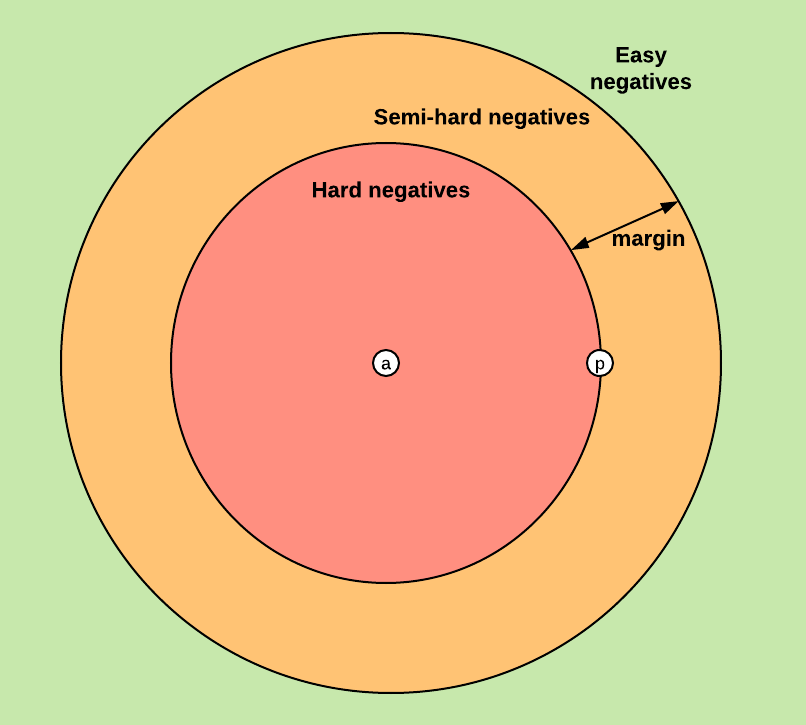Untitled 4 Source: https://omoindrot.github.io/triplet-loss

구현 코드는 아래와 같습니다.

class TripletLoss(nn.Module):
    """
    Triplet loss
    Takes embeddings of an anchor sample, a positive sample and a negative sample
    """

    def __init__(self, margin):
        super(TripletLoss, self).__init__()
        self.margin = margin

    def forward(self, anchor, positive, negative, size_average=True):
        distance_positive = (anchor - positive).pow(2).sum(1)
        distance_negative = (anchor - negative).pow(2).sum(1)
        losses = F.relu(distance_positive - distance_negative + self.margin)
        return losses.mean() if size_average else losses.sum()

Next

Triplet loss는 N개의 이미지에서 3개씩 조합을 찾는 경우, 양이 많아져서 매우 복잡해집니다. 또한 Easy Triplet의 경우 loss가 0이 되면서 훈련에 영향을 주지 않습니다. 따라서 위와 같은 Triplet 쌍을 Sampling하는 것은 의미가 없습니다.

FaceNet에서도 학습을 잘 시키기 위해 Semi-Hard Triplet을 만족하는 Sampling을 하였습니다. 좀 더 Smart한 Sampling방법이 필요하게 됩니다.

다음에는 어떻게 Sampling을 할 수 있을지를 살펴보겠습니다.

Reference